
June Huh, galardoado em 2022 com a medalha Fields, pela resolução original de várias conjecturas no campo da combinatória, como a de Dowling-Wilson e a de Heron-Rota-Welsh
June Huh, matemático do Institute for Advanced Study, Princeton (EUA), acaba de receber no Congresso Internacional de Matemáticos de 2022 a mais prestigiada distinção da Matemática: a medalha Fields.
Este prémio é-lhe atribuído, entre outros trabalhos, pela resolução original de várias conjecturas no campo da combinatória, como a de Dowling-Wilson e a de Heron-Rota-Welsh. Tão interessante como curioso é o facto das técnicas usadas por Huh para as demonstrações derivarem de uma área antiga e complexa - a Geometria Algébrica - que ninguém suspeitaria ser aplicável a este tipo de problemas combinatórios.
O aprendiz acidental
June Huh não teve um percurso tradicional como matemático. Filho de sul-coreanos, nasceu na Califórnia em 1983, onde os seus pais faziam uma pós-graduação, e viveu a sua infância em Seul. Em adolescente, queria ser poeta, mas gradualmente abandonou a ideia e pensou em tornar-se jornalista e divulgador de ciência. Decorria o ano de 2007, o seu último ano no curso de Astronomia e Física na Universidade de Seul, quando se matriculou numa disciplina avançada de Geometria leccionada pelo famoso matemático japonês Heisuke Hironaka; sem pensar muito na sua falta de pré-requisitos formais, a intenção de June era conhecer e entrevistar o famoso matemático.
Hironaka não ensinava Matemática de forma estática, nem sempre totalmente correcta: mostrava as dificuldades e o processo de tentativa e erro que faz parte da própria investigação. Foi isto que fascinou Huh, e o levou a ser aprendiz e, com o tempo, amigo do mestre japonês.
C(x) = - 4x + 8x2 - 5x3 + x4.
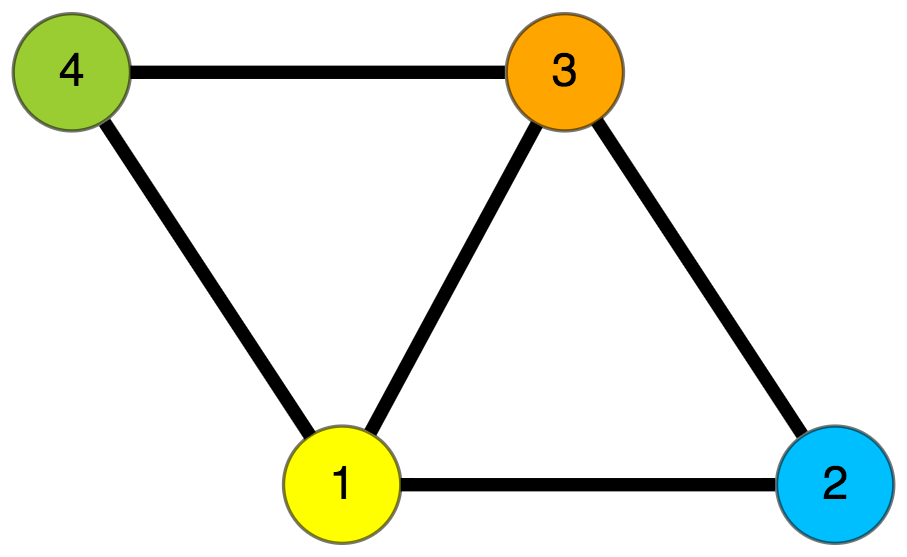
Note-se que C(1)=C(2)=0 o que mostra que não é possível colori-lo com uma ou duas cores apenas; mas C(3)=6 (desafio para o leitor: verifique que há seis colorações com três cores!). Os coeficientes (em valor absoluto) deste polínómio são:
(a0,...,a4)=(0, 4, 8, 5, 1) o que forma uma sequência unimodal uma vez que a0 < a1 < a2 > a3 > a4
Fonte CF
A conjectura de Heron-Rota-Welsh
Finalmente confiante para fazer um doutoramento, rumou de novo aos EUA. Foi aqui que se destacou após demonstrar uma conjectura sobre os polinómios cromáticos de grafos. Um grafo é um objecto composto de pontos, chamados vértices, e ligações entre os vértices, designados por arestas. O problema que Huh resolveu tem por base o polinómio cromático: este conta o número de colorações dos vértices de um grafo de forma que dois vértices ligados por uma aresta têm cores diferentes. Na figura, mostra-se um grafo e o seu polinómio cromático. Como vemos, o valor absoluto dos seus coeficientes, 0, 4, 8, 5, 1, formam uma sequência unimodal: primeiro crescente e depois decrescente (e apenas um máximo).
Desta forma, Huh demonstrou a conjectura de R. Read, de 1968, segundo a qual os coeficientes de qualquer polinómio cromático formam uma sequência unimodal. Uns anos mais tarde, orientado por Mircea Mustata, da Universidade de Michigan, e apercebendo-se que os grafos são casos particulares das estruturas combinatórias designadas por matróides, provou também a conjectura de Heron-Rota-Welsh: os polinómios característicos de qualquer matróide são unimodais (com E. Katz e K. Adiprasito [3]).
Aplicando Geometria Algébrica à resolução de problemas abertos em combinatória
Todos estes novos resultados, mesmo indirectamente, são consequência de uma rica estrutura geométrica que ninguém suspeitaria estar por detrás dos matróides: a geometria de variedades Kähler, espaços munidos de três estruturas geométricas compatíveis: a complexa, a simpléctica e a Riemanniana. De facto, a grande originalidade do trabalho de Huh pode ser descrita sucintamente como a descoberta de uma teoria de Hodge no contexto dos matróides.
O que motiva June Huh é a busca da beleza na Matemática, e a descoberta de ligações entre diferentes áreas desta disciplina. Com o seu percurso singular, ele mostra que mesmo encontrando a sua vocação mais tarde que outros colegas, é possível chegar ao mais alto nível mundial.
Referências
[1] https://www.quantamagazine.org/a-path-less-taken-to-the-peak-of-the-math-world-20170627/
[2] https://www.quantamagazine.org/june-huh-high-school-dropout-wins-the-fields-medal-20220705/
[3] Adiprasito, Karim; Huh, June; Katz, Eric Hodge theory for combinatorial geometries. Ann. of Math. (2) 188 (2018), no. 2, 381–452



























