No início do surto da COVID-19 em Portugal muitas vezes ouvi “mas o que pode dizer um matemático sobre epidemiologia?”. A resposta, que por vezes surpreendia o interlocutor, é muito, porque a dinâmica das epidemias é descrita por sistemas de equações diferenciais.
O mais simples dos modelos epidemiológicos foi desenvolvido em 1927 por Kermack e McKendrick. É o chamado “modelo SIR” devido aos nomes das três variáveis: susceptíveis, infectados, removidos. Os susceptíveis S(t) são os elementos da população que podem contrair a doença; os infectados I(t) são os que estão infectados e contagiosos; os removidos R(t) são os que recuperaram da doença e desenvolveram imunidade, ou morreram.
É simples, a partir do modelo SIR, provar que o surto inicial de uma doença para a qual a imunidade é nula, como era o caso da COVID-19, é exponencial. Partimos da equação para os infectados
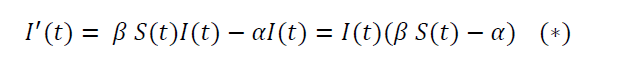
onde 1/a é o tempo de contágio e ß é a taxa de transmissão. Se no instante inicial t=0 não há imunidade, todos os indivíduos são susceptíveis; ou seja, S(0)=N, onde Né a população total. Nesse caso, enquanto o número de infectados I(t) for muito pequeno face a N, S (t) é aproximadamente igual a N. Seria o caso, por exemplo, com 100, 1.000 ou mesmo 10.000 infectados em Portugal (N=107). Substituindo na equação (*) S por N e resolvendo, obtemos
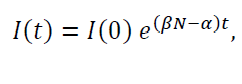
onde I (0) é o número de infectados em t=0. Daqui segue-se que existe o número de infectados cresce exponencialmente se (ßN-a)>0 ou seja, se
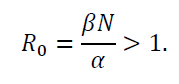
Nesta fase das nossas vidas, todos já ouvimos falar do famoso parâmetro R0. Eis a sua expressão no modelo SIR. O seu valor para a COVID-19 no início do surto em Portugal situava-se, dependendo das estimativas, entre 2,5 e 4. Aquilo que nos vimos obrigados a fazer para baixar o valor de R (confinamento, máscaras, higiene…) foram medidas de contenção para baixar o parâmetro ß, pois sobre os outros dois não temos controlo.
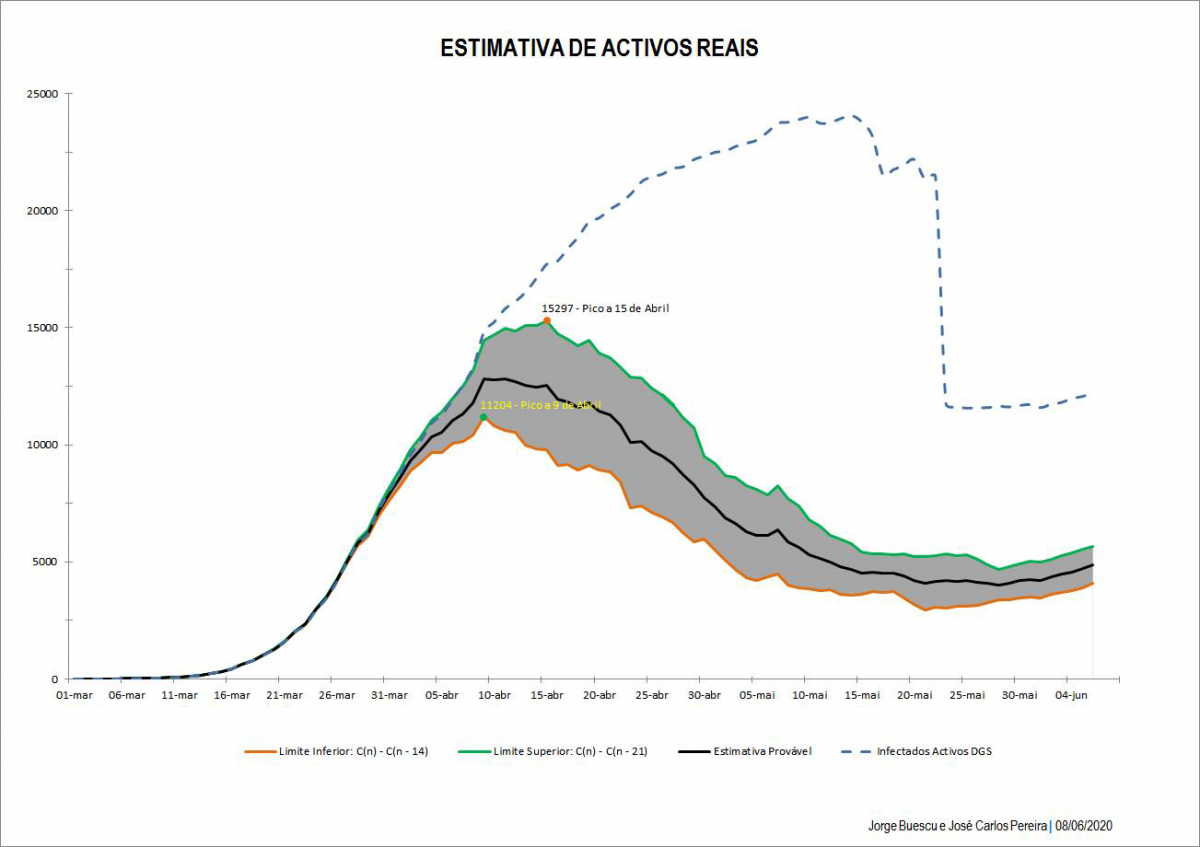
Como evoluiu a curva de infectados activos I(t) depois de tomarmos estas medidas? Para a calcular precisamos de subtrair, dos casos confirmados, os removidos (recuperados e mortos). Contudo, o número de recuperados nos boletins da Direção Geral da Saúde (DGS) rapidamente deixou de ser fiável. Assim, para reconstruir a curva de activos desenvolvemos (com apoio de José Carlos Pereira, alumnus da Ciências ULisboa) um método para estimar o seu número. Apresentamos o gráfico da curva epidemiológica reconstruída à data de 8 de Junho; para comparação, a tracejado está a curva que se obteria a partir dos dados da DGS; é bem visível o primeiro troço exponencial, antes das medidas de contenção. De acordo com esta estimativa o pico de activos terá ocorrido entre 9 e 15 de Abril, e a 1 de Junho cerca de 5.000 dos confirmados DGS estão activos; devido ao fenómeno dos assintomáticos o total de infectados activos poderá ser 5 a 10 vezes maior.